Babylonian mathematics is creating a buzz

26 September 2017

Among the hundreds of thousands of cuneiform tablets unearthed in the Near East, various groups of texts bear witness to the Babylonians’ knowledge of mathematics. The most important group of such tablets is composed of a thousand school exercises left behind by trainee scribes of the second millennium BCE, particularly in the town of Nippur, situated between the Tigris and Euphrates rivers in southern Iraq.

Some other texts dating from the same era are the products of scholars who wrote sequences of quadratic equations, or digital calculation algorithms, along with their respective solutions. One of these tablets, Plimpton 322, named after its lucky owner at the beginning of the twentieth century, which today is held by New York’s Columbia University, has intrigued scientists for more than 70 years.[1] The ancient text, which is not complete, provides a list of 15 triple numbers and shows for each of them their Pythagorean relationship, a relationship for which Franc-Nohain composed a quatrain: ‘Le carré de l’hypoténuse / est égal si je ne m’abuse / à la somme des carrés / construits sur les autres côtés.’ (The square of the hypotenuse [i.e. the side opposite the right angle] is equal to the sum of the squares of the other two sides.) 

The numbers that form the Pythagorean triples of Plimpton 322 are written using the sexagesimal positional number system peculiar to the writing of numbers in cuneiform mathematical texts. This number system, attested from the end of the third millennium BCE, is based on the use of two signs:

The upright wedge

, which represents 1. 

The head of a wedge

, which represents 10. 

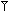
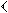
Numbers up to 59 are written by repeating these two signs, as required. This is a sexagesimal (base 60) number system.

60 is written the same way as 1, using a vertical wedge (

)

According to this system, the cuneiform number

can be read as 60 + 10 + 1 = 71.

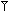
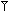
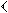
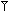
This is a positional number system since, based on the position they are placed in, the signs have different values. In the previous example, the upright wedge on the left has a value sixty times greater than that on the right.

No sign exists to represent an empty space, corresponding to our ‘zero’. This number system therefore does not specify the order of magnitude. Consequently, the vertical wedge only corresponds to a value of 1, 60, or 60 x 60, or all numbers to the power of 60, or 1/60.

The product of 30 multiplied by 4 is written thus:

, ‘2’, to be understood as 2 x 60 = 120.

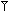
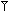
This provides a high degree of flexibility when making calculations, but at the same time calls for a good grasp of the size of the figures to be computed.

Plimpton 322 returned to the forefront this summer in an article published by two mathematicians from Sydney, Australia. These academics put forward the suggestion that the tablet in fact bore the very first trigonometric table, one and a half thousand years before that offered by the Greek mathematician Hipparchus (second century BCE).[2] A trigonometric table furnishes the relationships between the value of angles and the lengths of the sides of right-angle triangles. Plimpton 322 contains no data on the said angles. Such a proposition fails to take into account the historical context in which this particular tablet was generated; however, some other tablets produced by mathematicians in southern Mesopotamia at the beginning of the second millennium BCE discovered to date make it possible to support such a hypothesis.

On Plimpton 322, each Pythagorean triple is composed of whole numbers, some of which contain up to eight sexagesimal positions. These triples therefore correspond to right-angle triangles whose length, width and diagonal correspond to whole numbers. According to Britton, Proust and Shnider (2011), they could have been obtained through an algorithm used by Babylonian scribes, a vestige of which one finds in the texts deciphered by Jöran Friberg. The fifteen visible lines form part of the solution to an arithmetic problem; the uninscribed part of the tablet (its reverse) could have been prepared to receive the missing part of the solution. Other cuneiform tablets dating from this period exist which contain digital calculation algorithms, together with their solutions.

Each cuneiform text, taken alone, furnishes certain types of information that then has to be compared against texts produced in the same environment, a step that enables the historian to either validate or debunk their hypotheses, so as to gain a better idea of the text’s author and of the environment in which it developed. When a text is sold on the ancient antiquities market, on the one hand it is effectively severed from its archaeological context, and on the other from the collection of texts in which it was kept. According to the Assyriologist E. J. Banks, who sold the tablet in question to George Arthur Plimpton in 1922, it originated from Larsa, in southern Mesopotamia, a site which in all likelihood yielded an entire batch of scholarly mathematical tablets … all of which have ended up on the antiquities market.

[1] The most recent articles are by Britton, John P., Proust Christine, Shnider, Steve (2011), ‘Plimpton 322: A Review and a Different Perspective’, Archive for History of Exact Sciences, Archive for History of Exact Sciences, 65/5, 519-566; Robson, Eleonore (2001), ‘Neither Sherlock Holmes nor Babylon: A Reassessment of Plimpton 322’, Historia Mathematica 28/3, 167-206.

[2] Mansfield, Daniel F. and Wildberger, Norman J. (2017), Plimton 322 is Babylonian exact sexagesimal trigonometry, Historia Mathematica, 44/4.